2024-09-30
The Beginning of Humanity's Last Invention
I recently decided to go back and relearn how different concepts in AI and machine learning actually work. At some point, I realized that my understanding wasn't as concrete as I'd thought - it was more like I know about the concepts, but not really understand how they worked under the hood. So, I figured it was time to dive straight into the mathematics and logic behind these models.
As I went through this process, I remembered a quote by Richard Feynman: "If you want to master something, teach it." That's what inspired me to write this piece. By breaking down the inner workings of neural networks, I hope to not only solidify my own understanding and also offer a resource for others who want to grasp the fundamental mechanics of these incredible models.
Part 1: Forward Propagation
Think of a neural network as a mathematical function that takes in an input and produces an output . Our goal is to compute the output , which we represent as . However, to allow our neural networks to capture complex patterns in data, we introduce two key parameters: weights and biases .
These parameters play roles similar to those in a linear equation, like , where is the slope and is the intercept. In this case, the weights control how much influence each input has on the output, and the bias shifts the output.
Example with a Single Neuron
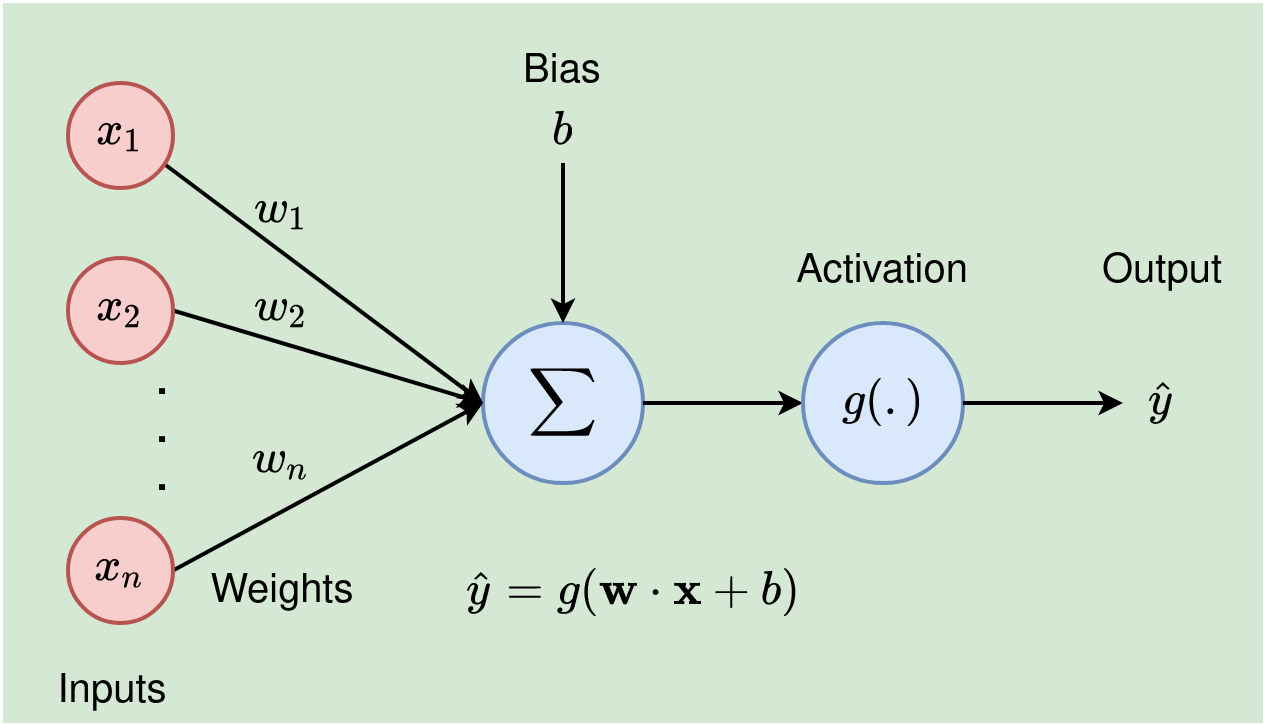
Figure 1: Visualization of a single neuron in a neural network. The inputs are multiplied by their corresponding weights and summed along with a bias . The sum is then passed through an activation function to produce the output . Source here
Let's start with a simple example: a single neuron. Suppose we have three inputs . Each input is multiplied by a corresponding weight and then summed together. To this sum, we add a bias term. We can write the neuron's output as:
This equation shows how the inputs are weighted and summed, with the bias adjusting the final value. But neural networks rarely consist of just one neuron. To tackle more complex problems, we typically use multiple neurons.
Mathematical Representation of Forward Propagation
When we have multiple neurons in a layer, we use matrix operations to represent forward propagation. For a layer with several neurons, the output is given by:
Where:
- is a matrix of weights (each row corresponds to a neuron),
- is the input vector,
- is the bias vector (one bias per neuron).
This equation can be interpreted as each input being multiplied by its corresponding weight , and the results are added to the bias. This process is repeated for all neurons, and the resulting outputs are summed.
Derivation of Forward Propagation Formula
Let's break this down with a simple example. Suppose we have three inputs, , each paired with a weight . After multiplying each input by its respective weights, we add the bias term. This can be expressed as:
This simplifies to the equation:
For a dataset with examples, the equation generalizes to:
Activation Functions: Adding Non-Linearity
Once we compute the weighted sum, we pass the result through an activation function. This step introduces non-linearity, which is crucial because it allows the network to model more complex patterns beyond what a simple linear function can achieve.
Popular activation functions include Sigmoid and Tanh, but here we'll focus on the Rectified Linear Unit (ReLU), which is commonly used in modern neural networks. The ReLU activation function works as follows:
- If the input is greater than 0, it returns ,
- If is less than or equal to 0, it returns 0.
Mathematically, this can be written as:
ReLU is effective because it introduces non-linearity while being simple to compute.
Summary of the Forward Propagation Process
To summarize, the forward propagation process involves:
- Input Transformation: Inputs are multiplied by weights and added to biases, creating a weighted sum.
- Activation: The weighted sum is passed through an activation function to introduce non-linearity.
- Output: The final value is the neuron's output, which can be passed to the next layer or used as the network's prediction.
Part 2: Cost Function - Measuring Prediction Quality
Once our neural network has made a prediction, the next step is to measure how accurate the prediction is. To do this, we use a cost function. The cost function provides a way to quantify how far the prediction is from the actual value, and our objective is to minimize this error over time.
One widely used cost function is the Mean Squared Error (MSE). The formula for MSE is:
Where:
- is the predicted value,
- is the actual value,
- is the number of samples, and
- is the cost (or error) that we want to minimize.
Intuition Behind MSE
The Mean Squared Error measures the average squared difference between the predicted and actual values. By squaring the difference, we ensure that larger errors are penalized more heavily. Squaring also guarantees that all errors are positive, regardless of whether the prediction is too high or too low.
Mathematical Proof of MSE
Let’s break down the MSE calculation step by step:
-
Calculate the Difference: For each prediction , subtract the actual value . This difference is the prediction error.
-
Square the Difference: To ensure that all errors are positive and to give larger errors more weight, we square the differences:
-
Sum Over All Predictions: For models with multiple predictions, we sum these squared errors:
-
Average the Errors: To find the average squared error, divide the sum by the number of predictions:
The goal of training is to minimize , reducing the difference between predictions and true values.
Throughout the training process, the objective is to minimize . By doing so, we aim to reduce the overall error between the predictions made by the model and the actual target values.
Part 3: Backpropagation - Learning from Mistakes
So far, we've learned how a neural network makes predictions and measures their accuracy. However, none of this is useful unless the model can learn from its mistakes and improve. This is where backpropagation comes in.
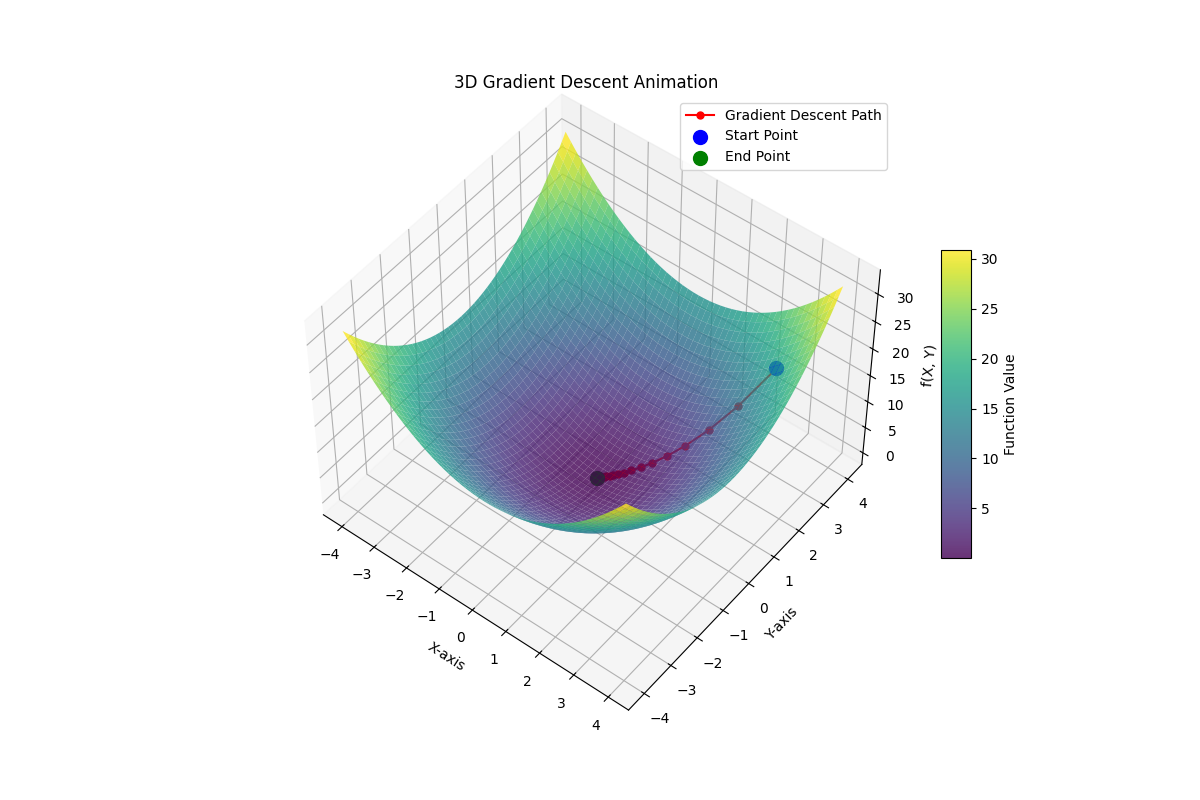 Figure 2: Visualization of the gradient descent process on a 3D error surface. The path shows the iterative steps taken by the algorithm as it moves from the initial point (blue) towards the global minimum (green), minimizing the error (cost) at each step.
Figure 2: Visualization of the gradient descent process on a 3D error surface. The path shows the iterative steps taken by the algorithm as it moves from the initial point (blue) towards the global minimum (green), minimizing the error (cost) at each step.
Backpropagation is the process that allows the model to adjust its internal parameters—weights and biases—to minimize the cost function. This adjustment is guided by the gradients of the cost function with respect to the weights and biases.
The update rule for these parameters is:
Where:
- represents the weights and biases,
- is the learning rate, and
- is the gradient of the cost function.
Mathematical Proof of Backpropagation
Backpropagation works by moving backwards through the network to calculate the necessary adjustments to the weights and biases. Let's break this process down step by step:
Before diving into the backpropagation steps, let's quickly recap some key notations:
-
Weighted input:
-
Activation:
Where:
- is the activation function (applied element-wise),
- is the activation from the previous layer,
- is the weight matrix, and
- is the bias vector.
The goal now is to compute:
efficiently, where is the cost function.
Equation 1: Output Layer Error
Explanation:
- represents the error in the output layer (layer ).
- is the derivative of the cost function with respect to the activation in the output layer.
- is the derivative of the activation function with respect to the weighted input .
Derivative:
-
We want to compute how the cost function changes with respect to the weighted input .
-
Using the chain rule, we can expand this as:
Backpropagation Tie-In:
- This equation initializes the backpropagation process by calculating the error at the output layer. It shows how the network's final prediction affects the cost and sets up the error to be propagated backward.
Equation 2: Hidden Layer Error
Explanation:
- represents the error at the hidden layer .
- is the weighted sum of the errors from the next layer .
- adjusts this error based on the activation function's derivative at layer .
Derivative:
-
To compute how the cost changes with respect to the inputs of the current layer, we use the chain rule:
Backpropagation Tie-In:
- This recursive formula allows us to propagate the error backward through each hidden layer. It effectively updates the error term, which we will use to adjust the weights and biases.
Equation 3: Gradient with Respect to Bias
Explanation:
- The gradient of the cost function with respect to the bias at layer is simply the error at that layer.
Derivative:
-
By applying the chain rule, we get:
-
From Equation 2, we know that , and .
Backpropagation Tie-In:
- Once we have , we directly obtain the gradient of the bias. This not only simplifies the computation but also enables straightforward updates to the bias in each layer during training.
Equation 4: Gradient with Respect to Weights
Explanation:
- This equation shows how the cost function changes with respect to the weights in layer . The gradient is the product of the error and the activation from the previous layer, .
- The expression is the transpose of the activations, ensuring the gradient has the correct dimensions for the weight matrix.
Derivative:
-
To find how the cost changes with respect to the weights, we use the chain rule:
-
From Equation 2, we know that , and .
Backpropagation Tie-In:
- This equation is crucial as it shows how the weights in each layer contribute to the cost. By using the gradient, we can update the weights during training to reduce the error.
Visual Representation of the Backpropagation Process
-
Forward Pass: Compute and for each layer up to the output layer . This step involves applying weights, biases, and activation functions to generate the network's output.
-
Backward Pass:
- Output Layer (Layer ): Compute the error using Equation 1.
- Hidden Layers: Starting from layer and moving backward to layer 1, compute for each hidden layer using Equation 2. This step propagates the error back through the network.
-
Gradient Computation: For each layer :
-
Calculate the gradient with respect to the biases using Equation 3:
-
Calculate the gradient with respect to the weights using Equation 4:
-
-
Parameter Update:
-
Adjust the weights and biases using the computed gradients. For example, with gradient descent:
-
Where is the learning rate.
-
Explanation:
- This visual guide outlines the main steps of the backpropagation process, highlighting how errors are propagated backward and how gradients are used to update parameters.
- By repeating these steps across multiple iterations, the network learns to reduce the overall cost, improving its predictions.
Part 4: Hand Computation
In this section, we’ll manually compute a simple neural network's forward and backward passes to build a deeper understanding of the calculations.
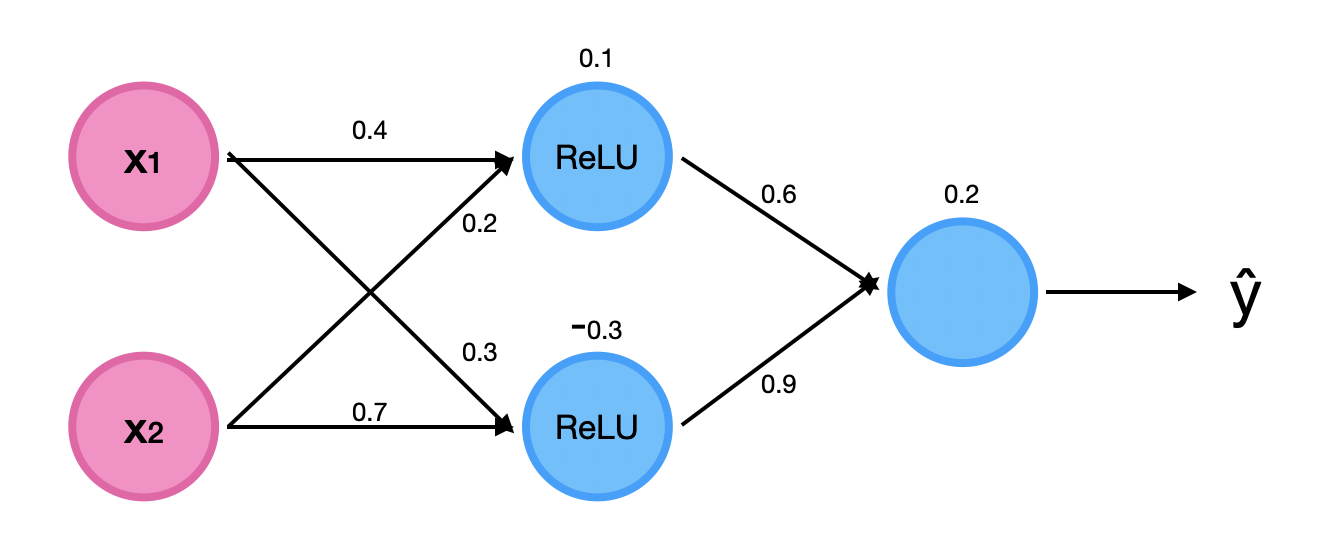
Network Structure:
- Inputs: ,
- Hidden Layer: 2 neurons
- Output Layer: 1 neuron
- True Output:
- Learning Rate:
Weights and Biases:
-
From input to hidden layer:
-
From hidden to output layer:
Step 1: Forward Propagation
-
Input to Hidden Layer Calculation:
-
First, we compute the weighted input to the hidden layer:
-
Substituting the values, we get:
-
-
Activation (ReLU) for Hidden Layer:
-
Apply the ReLU activation function to each element of :
-
Here, ReLU returns 0 for negative inputs and the input itself for positive values.
-
-
Hidden to Output Layer Calculation:
-
Next, we compute the weighted input to the output layer:
-
Substituting the values, we get:
-
-
Final Output:
- Since we're not applying an additional activation function at the output layer, our final output for this forward pass is 0.392.
Step 2: Cost Calculation
-
To measure how far off our prediction is from the actual output, we use the Mean Squared Error (MSE):
-
This cost value indicates the error in the current predictions, which we will now work to minimize using backpropagation.
Step 3: Backward Propagation
-
Output Layer Error:
-
Using the chain rule and the derivative of the cost function, the error term for the output layer is:
-
-
Update Bias for Output Layer:
-
The gradient with respect to the bias at the output layer is simply the error term:
-
Update the bias using gradient descent:
-
-
Update Weights for Output Layer:
-
The gradient with respect to the weights is:
-
Update the weights:
-
-
Hidden Layer Error:
-
Calculate the error term for each neuron in the hidden layer:
-
-
Update Bias for Hidden Layer:
-
For the first neuron:
-
For the second neuron, no change as :
-
-
Update Weights for Hidden Layer:
-
For the first hidden neuron:
-
Update the weights:
-
For the second hidden neuron, no change:
-
Conclusion
These steps illustrate how a neural network learns through forward propagation, cost evaluation, and backpropagation. By manually updating the weights and biases, we gain a clearer understanding of how the model gradually improves its predictions. This process repeats over many iterations, reducing the error and fine-tuning the network's performance.
Closing Thoughts
Neural Networks have shown they can learn just about anything, from recognizing faces in photos to translating languages. As Geoffrey Hinton, one of the pioneers in deep learning, put it: "Neural Networks are capable of learning anything if you give them enough data and compute." This really shows how flexible and powerful these systems are.
With all the excitement around artificial intelligence today, especially with the rise of large language models (LLMs), it's more important than ever to understand how neural networks actually work. And as we push forward in the race towards Artificial General Intelligence (AGI), knowing the ins and outs of these networks gives us a better grip on where we're headed. By understanding the nuts and bolts of neural networks, we can ensure we're using this technology wisely and steering it in the right direction.